QAOA and Maximum Cut Problem

1. Problem Statement

The goal of maximum cut is to split the set of vertices \(V\) of a graph into two disjoint parts such that the number of edges spanning two parts is maximized.

For example, if color denotes part, in the graph on the following 4 edges are cut:

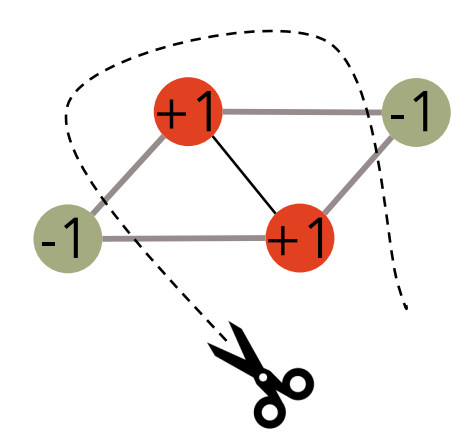
Maximum cut can be formulated as an optimization problem:

\[\max _{\mathbf{s}} \frac{1}{2} \sum_{i j \in E}\left(1-s_{i} s_{j}\right) \quad s_{i} \in\{-1,+1\}\]

• \[\text { Same sign - no edge is cut (no contribution to the objective): } \frac{1}{2}\left(1-s_{i} s_{j}\right)=0\]
• \[\text { Different sign - an edge is cut (contribution to the objective }=1): \frac{1}{2}\left(1-s_{i} s_{j}\right)=1\]

1.1 Example

For the following example, the answer would be that six edges are cut.

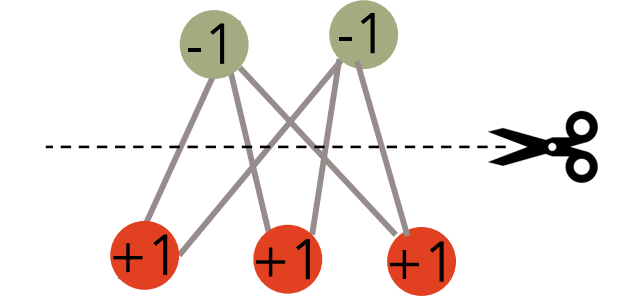
2. Solving Combinatorial Optimization Problems on a Quantum Computer

Maximizing objective:

\[\max _{\mathbf{s}} C(\mathbf{s})=\frac{1}{2} \sum_{i j \in E}\left(1-s_{i} s_{j}\right)\]

Objective in Quantum Computing: Characterizing a Hamiltonian (Hermitian operator) \(C\)

To solve an optimization problem on a quantum computer, we need to convert it into a problem of characterizing a quantum Hamiltonian.

The classical solution would be some \(\mathbf{s} \in\{-1,+1\}^{n}\)

. The quantum solution would be the highest energy eigenstate \(\vert s \rangle\) with the largest eigenvalue.

Since the Hamiltonian is classical, this eigenstate is a computational basis state*, we can measure it and get the solution with certainty.

2.1 What does this Hamiltonian look like?

Hamiltonian is diagonal, with values on the diagonal corresponding to the values of the objective function.

As we discussed, our objective function is: \(\max _{x \in\{0,1\}^{n}} f(x)\)

We would construct a hamiltonian function:

\[C=\left(\begin{array}{ccccc} f(0 \ldots 00) & 0 & 0 & 0 & 0 \\ 0 & f(0 \ldots 01) & 0 & 0 & 0 \\ \vdots & & \ddots & & \\ 0 & 0 & 0 & f(1 \ldots 10) & 0 \\ 0 & 0 & 0 & 0 & f(1 \ldots 11) \end{array}\right)\] \[C\vert x\rangle=\left(\begin{array}{ccccc} f(0 \ldots 00) & 0 & 0 & 0 & 0 \\ 0 & f(0 \ldots 01) & 0 & 0 & 0 \\ \vdots & & \ddots & & \\ 0 & 0 & 0 & f(1 \ldots 10) & 0 \\ 0 & 0 & 0 & 0 & f(1 \ldots 11) \end{array}\right)\left(\begin{array}{c} 0 \\ \vdots \\ 1 \\ \vdots \\ 0 \end{array}\right)=f(x)\vert x\rangle \quad \forall x \in\{0,1\}^{n}\]

This Hamiltonian is too large to construct explicitly!

2.1 How do we construct this Hamiltonian?

• MAXCUT objective: \(\max _{\mathbf{s}} \frac{1}{2} \sum_{i j \in E}\left(1-s_{i} s_{j}\right) \quad s_{i} \in\{-1,+1\}\)
• MAXCUT Hamiltonian is constructed by mapping binary variables \(s_{i}\) onto the eigenvalues of \(Z\)

\(C=\frac{1}{2} \sum_{i j \in E}\left(I-Z_{i} Z_{j}\right)\)

• Want to show:
• \[C\vert x\rangle=C(\mathbf{x})\vert x\rangle\]

Why we use Pauli Z operator?

• Consider Pauli Z operator \(Z=\left[\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right]\)

• Note that it has eigenvalues \(-1,+1\) with eigenvectors being computational basis states \(\begin{aligned} &Z\vert 0\rangle=\left[\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right]\left[\begin{array}{l} 1 \\ 0 \end{array}\right]=\left[\begin{array}{c} 1 \\ 0 \end{array}\right]=\vert 0\rangle \\ &Z\vert 1\rangle=\left[\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right]\left[\begin{array}{l} 0 \\ 1 \end{array}\right]=\left[\begin{array}{c} 0 \\ -1 \end{array}\right]=(-1)\vert 1\rangle \end{aligned}\)

Therefore,

\[Z\vert x\rangle=(-1)^{x}\vert x\rangle \quad x \in\{0,1\}\]

• Acting on the i-th qubit: \(\begin{aligned} Z_{i}\left\vert x_{0} \ldots x_{n}\right\rangle &=I \otimes \ldots \otimes Z_{i} \otimes \ldots \otimes I\left\vert x_{0} \ldots x_{n}\right\rangle \\ &=(-1)^{x_{i}}\left\vert x_{0} \ldots x_{n}\right\rangle \quad x_{i} \in\{0,1\}, \quad i=1, \ldots n \end{aligned}\)

• Acting on the \(\mathrm{i}\)-th and \(\mathrm{j}\)-th qubit: \(\begin{aligned} Z_{i} Z_{j}\left\vert x_{0} \ldots x_{n}\right\rangle &=I \otimes \ldots \otimes Z_{i} \otimes Z_{j} \otimes \ldots \otimes I\left\vert x_{0} \ldots x_{n}\right\rangle \\ &=(-1)^{x_{i}}(-1)^{x_{j}}\left\vert x_{0} \ldots x_{n}\right\rangle \quad x_{i} \in\{0,1\}, \quad i=1, \ldots n \end{aligned}\)

MAXCUT Hamiltonian is constructed by mapping binary variables si onto the eigenvalues of Z.

• MAXCUT objective:

\[\max _{\mathbf{s}} \frac{1}{2} \sum_{i j \in E}\left(1-s_{i} s_{j}\right) \quad s_{i} \in\{-1,+1\}\]

• Let’s reformulate it in the following way:

\[\begin{gathered} x_{i}=\frac{1}{2}\left(1-s_{i}\right) \\ s_{i}=1 \rightarrow x_{i}=0, \quad(-1)^{x_{i}}=1=s_{i} \\ s_{i}=-1 \rightarrow x_{i}=1, \quad(-1)^{x_{i}}=-1=s_{i} \end{gathered}\]

• New objective:

\[\max _{\mathbf{x}} \frac{1}{2} \sum_{i j \in E}\left(1-(-1)^{x_{i}}(-1)^{x_{j}}\right) \quad x_{i} \in\{0,1\}\] \[\begin{aligned} C\vert x\rangle &=\frac{1}{2} \sum_{i j \in E}\left(I-Z_{i} Z_{j}\right)\left\vert x_{0} \ldots x_{n}\right\rangle \\ &=\frac{1}{2} \sum_{i j \in E}\left(I-Z_{i} Z_{j}\right)\left\vert x_{0} \ldots x_{n}\right\rangle \\ &=\frac{1}{2} \sum_{i j \in E}\left(\left\vert x_{0} \ldots x_{n}\right\rangle-Z_{i} Z_{j}\left\vert x_{0} \ldots x_{n}\right\rangle\right) \\ &\left.=\frac{1}{2} \sum_{i j \in E}(1-(-1)^{x_{i}}(-1)^{x_{j}}\right) \left\vert x_{0} \ldots x_{n}\right\rangle=C(\mathbf{x})\vert x\rangle \\ x_{i} & \in\{0,1\}, \quad i=1, \ldots n \end{aligned}\]

3. Quantum Approximate Optimization Algorithm

• OAOA prepares a parameterized “trial” (ansatz) state of the form:

\[\begin{aligned} \vert \psi(\boldsymbol{\theta})\rangle &=\vert \psi(\boldsymbol{\beta}, \gamma)\rangle \\ &=e^{-i \beta_{p} B} e^{-i \gamma_{p} C} \cdots e^{-i \beta_{1} B} e^{-i \gamma_{1} C} H^{\otimes n}\vert 0\rangle \end{aligned}\]

• Here \(C\) is the problem Hamiltonian, e.g. for MAXCUT: \(C=\frac{1}{2} \sum_{i j \in E}\left(I-Z_{i} Z_{j}\right)\)

• \(B\) is the mixer Hamiltonian: \(B=\sum_{i} X_{i}\)

Why do we need a mixer Hamiltonian operator:

Preserve the feasibility and explore possible solutions. If we have some constraints on the problems, we can encode them by mixer operators.

Why do we need p layer to this circuit?

Actually, we can use only one layer to optimize this circuit on universal quantum computers. The reason that we still use p is that it would perform better if we use quantum-annealing computers.

Then a classical optimizer is used to vary the parameters \(\boldsymbol{\beta}, \boldsymbol{\gamma}\) to maximize:

\[f(\boldsymbol{\beta}, \boldsymbol{\gamma})=\langle\psi(\boldsymbol{\beta}, \boldsymbol{\gamma})\vert C\vert \psi(\boldsymbol{\beta}, \boldsymbol{\gamma})\rangle\]

Note that for p → ∞ QAOA can at least exactly approximate adiabatic quantum evolution and can therefore find the exact optimal solution • For small p, picture is more mixed, but there is some indication of the potential for quantum advantage.

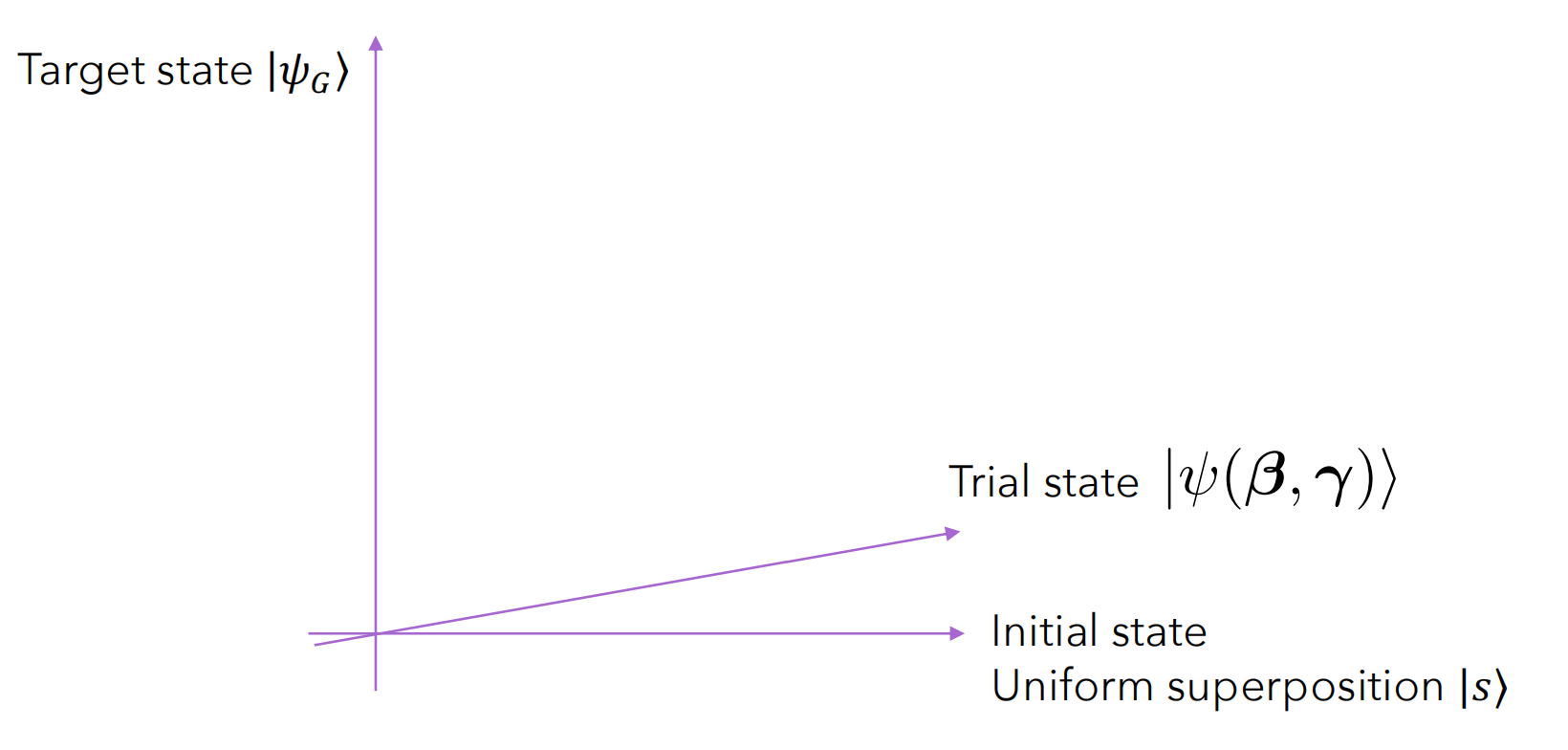
Crucially, the quality of QAOA solution heavily depends on the quality of the parameters found by the classical optimizer

4. Constructing a Hamiltonian for a general problem

How can we do this efficiently for an arbitrary function \(f\)? In other words, how do we map Boolean and real functions to diagonal Hamiltonians acting on qubits?

To be updated.

5. How can we implement QAOA on quantum circuits?

To be updated.

Reference:

1. Nielsen, Michael A., and Isaac Chuang. "Quantum computation and quantum information." (2002): 558-559.

2. Asfaw, Abraham, et al. "Learn quantum computation using qiskit." Accessed: Oct 24 (2020): 2020.

3. Susskind, Leonard, and Art Friedman. Quantum mechanics: the theoretical minimum. Basic Books, 2014.

4. On the representation of Boolean and real functions as Hamiltonians for quantum computing." arXiv preprint arXiv:1804.09130 (2018).

​