1. Problem Statement
If we have a periodic function \(f(x)=a^{x}(\bmod N)\) (Following figure), how can we find the order \(r\) in a quantum algorithm?
- For example, \(a^{0}(\bmod N)=1\) and \(a^{r}(\bmod N)=1.\)
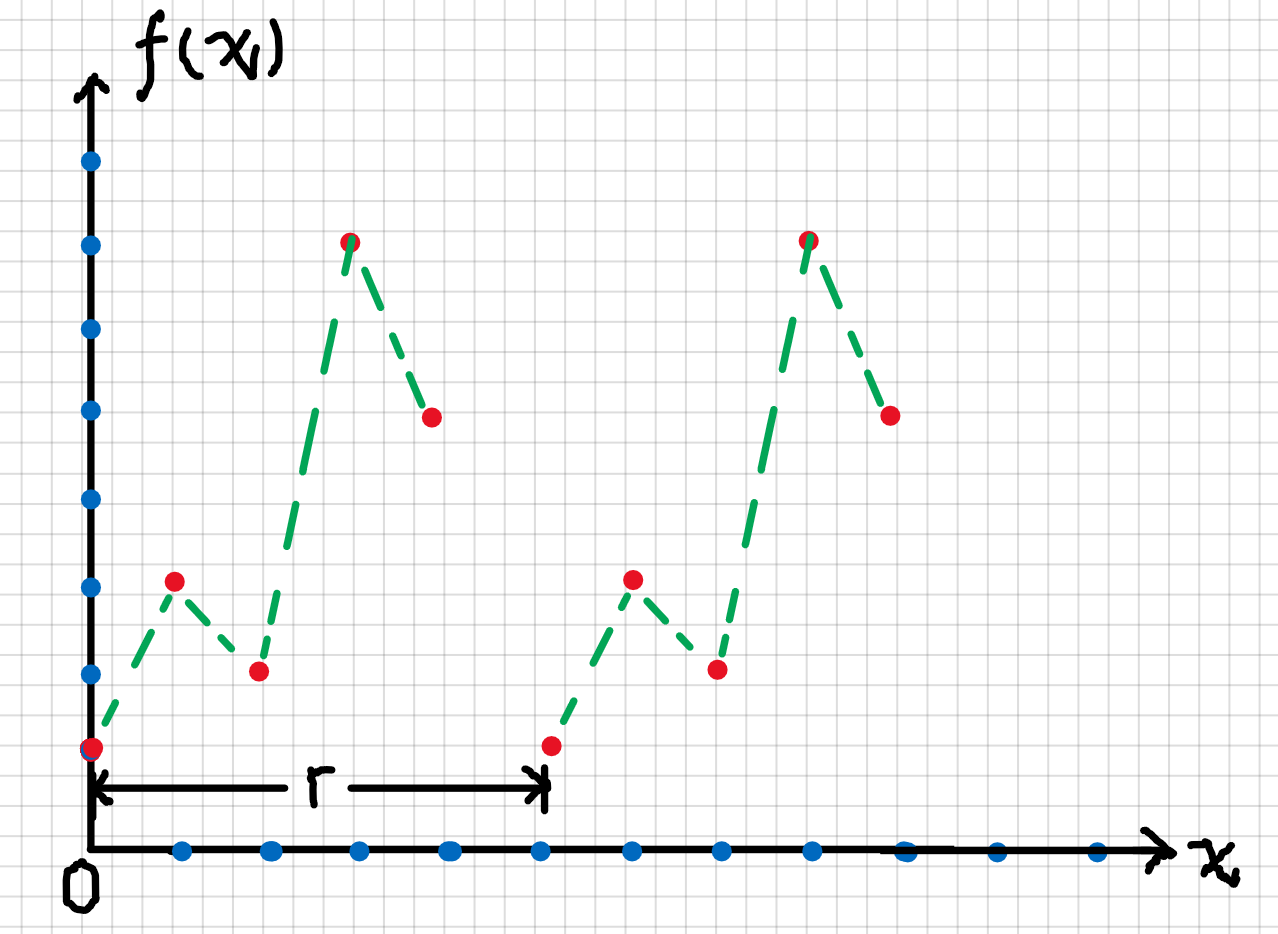
Order-finding is believed to be a hard problem on a classical computer, in the sense that no algorithm is known to solve the problem using resources polynomial in the \(O(L)\) bits needed to specify the problem, where \(L \equiv\lceil\log (N)\rceil\) is the number of bits needed to specify \(N\).
2. Circuit Design
Inputs:
(1) A black box \(U_{x, N}\) which performs the transformation \(\vert j\rangle\vert k\rangle \rightarrow\vert j\rangle\left\vert x^{j} k \bmod N\right\rangle\), for \(x\) co-prime to the \(L\)-bit number \(N\)
(2) \(t=2 L+1+\left\lceil\log \left(2+\frac{1}{2 \epsilon}\right)\right\rceil\) qubits initialized to \(\vert 0\rangle\)
(3) \(L\) qubits initialized to the state \(\vert 1\rangle\). Outputs: The least integer \(r>0\) such that \(x^{r}=1(\bmod N)\).
Runtime: \(O\left(L^{3}\right)\) operations. Succeeds with probability \(O(1)\).
Procedure:
- initial state \(\vert 0\rangle\vert 1\rangle\)
- create superposition \(\rightarrow \frac{1}{\sqrt{2^{t}}} \sum_{j=0}^{2^{t}-1}\vert j\rangle\vert 1\rangle\)
- apply \(U_{x, N}\) \(\rightarrow \frac{1}{\sqrt{2^{t}}} \sum_{j=0}^{2^{t}-1}\vert j\rangle\left\vert x^{j} \bmod N\right\rangle\) \(\approx \frac{1}{\sqrt{r 2^{t}}} \sum_{s=0}^{r-1} \sum_{j=0}^{t^{t}-1} e^{2 \pi i s j / r}\vert j\rangle\left\vert u_{s}\right\rangle\)
- apply inverse Fourier transform to first register \(\rightarrow \frac{1}{\sqrt{r}} \sum_{s=0}^{r-1} \widehat{s / r} \mid\left\langle u_{s}\right\rangle \quad\)
- measure first register \(\rightarrow \widehat{s / r}\)
- apply continued fractions algorithm \(\rightarrow r\)
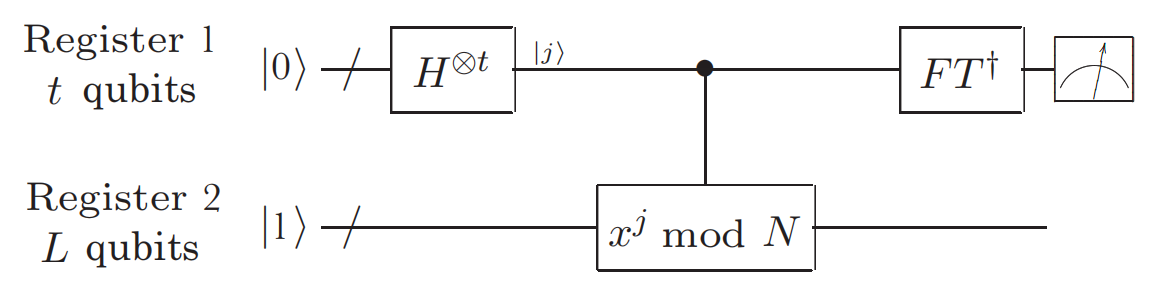
The quantum algorithm for order-finding is just the phase estimation algorithm applied to the unitary operator \(U\vert y\rangle \equiv\vert x y(\bmod N)\rangle\)
\[(0 \leq y \leq N-1.)\]Then let’s see what are the eigenvectors and eigenvalues of operator \(U\).
A simple calculation shows that the states defined by
\[\left\vert u_{s}\right\rangle \equiv \frac{1}{\sqrt{r}} \sum_{k=0}^{r-1} \exp \left[\frac{-2 \pi i s k}{r}\right]\left\vert x^{k} \bmod N\right\rangle,\]for integer \(0\leq s\leq r-1\) are eigenstates of \(U\), since
\[\begin{aligned} U\left\vert u_{s}\right\rangle &=\frac{1}{\sqrt{r}} \sum_{k=0}^{r-1} \exp \left[\frac{-2 \pi i s k}{r}\right]\left\vert x^{k+1} \bmod N\right\rangle \\ &=\exp \left[\frac{2 \pi i s}{r}\right]\left\vert u_{s}\right\rangle \end{aligned}\]Using the phase estimation procedure allows us to obtain, with high accuracy, the corresponding eigenvalues \(\exp (2 \pi i s / r)\), from which we can obtain the order \(r\) with a little bit more work.
Then our idea would be use operator U to convert the system into \(\vert u \rangle\) basis.
But we do not know what is r then how can we prepare state \(\vert u \rangle\).
The answer is preparing \(\left\vert u_{s}\right\rangle\) requires that we know \(r\), so this is out of the question. Fortunately, there is a clever observation which allows us to circumvent the problem of preparing \(\left\vert u_{s}\right\rangle\), which is that
\[\frac{1}{\sqrt{r}} \sum_{s=0}^{r-1}\left\vert u_{s}\right\rangle=\vert 1\rangle .\]In performing the phase estimation procedure, if we use \(t=2 L+1+\left\lceil\log \left(2+\frac{1}{2 \epsilon}\right)\right\rceil\) qubits in the first register and prepare the second register in the state \(\vert 1\rangle\). It follows that for each \(s\) in the range 0 through \(r-1\), we will obtain an estimate of the phase \(\varphi \approx s / r\) accurate to \(2 L+1\) bits, with probability at least \((1-\epsilon) / r\).
Now let’s think does L qubits satisfy enough information about state \(\vert u \rangle\) ?
We have seen that \(L \equiv\lceil\log (N)\rceil\), so \(2^{L}>N\). Besides, we know that we need r different states for all basis. So we oeed to prove that \(N>r\). According to Euler’s theorem, \(N > r\), which will not be proved in this part.
The other thing I want to discuss here is Modular exponentiation. How can operator U work?
Based on the following figure, the final state of the first register is easily seen to be:
\[\begin{aligned} \frac{1}{2^{t / 2}}\left(\vert 0\rangle+e^{2 \pi i 2^{t-1} \varphi}\vert 1\rangle\right)\left(\vert 0\rangle+e^{2 \pi i 2^{t-2} \varphi}\vert 1\rangle\right) & \ldots\left(\vert 0\rangle+e^{2 \pi i 2^{0} \varphi}\vert 1\rangle\right) \\ &=\frac{1}{2^{t / 2}} \sum_{k=0}^{2^{t}-1} e^{2 \pi i \varphi k}\vert k\rangle . \end{aligned}\]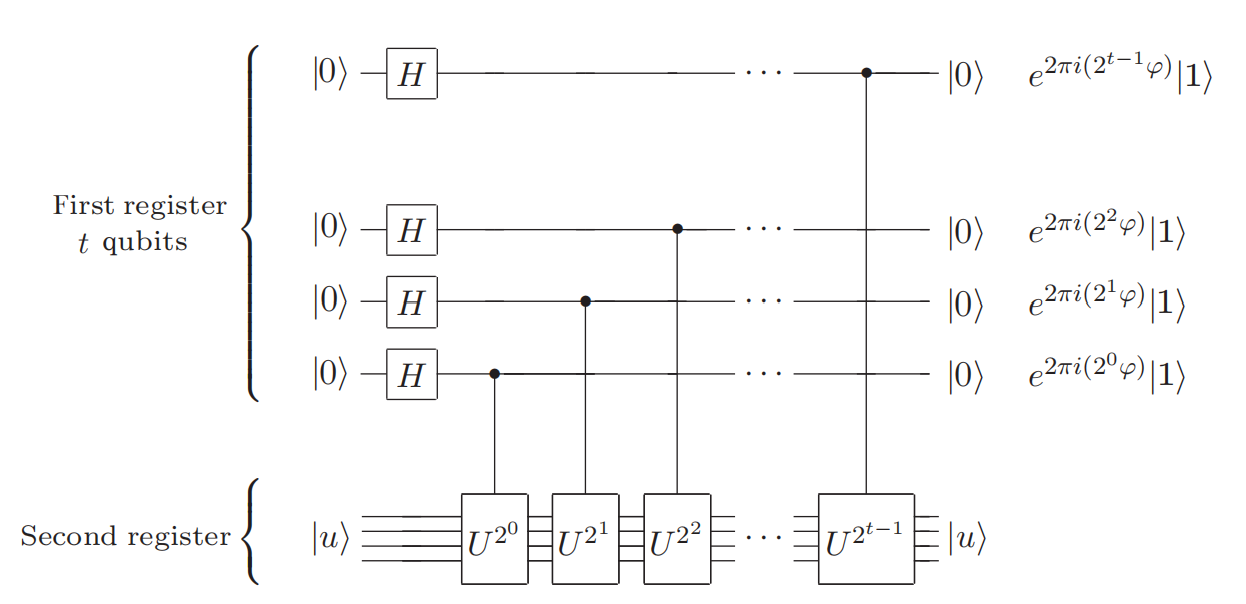
Therefore, we only need use controlled-\(U^{2^{j}}\) to rotate different qubits we can result a system we want.
So by our circuit, we can get is \(\frac{s}{r}\), then we need to estimate what is r by the continued fraction expansion. We will use am example to show how can we use continued fraction expansion.
3. An Example for order-finding
In this example we will solve the period finding problem for \(a=7\) and \(N=15\). We provide the circuits for \(U\) where:
\[U\vert y\rangle=\vert a y \bmod 15\rangle\]without explanation. To create \(U^{x}\), we will simply repeat the circuit \(x\) times.
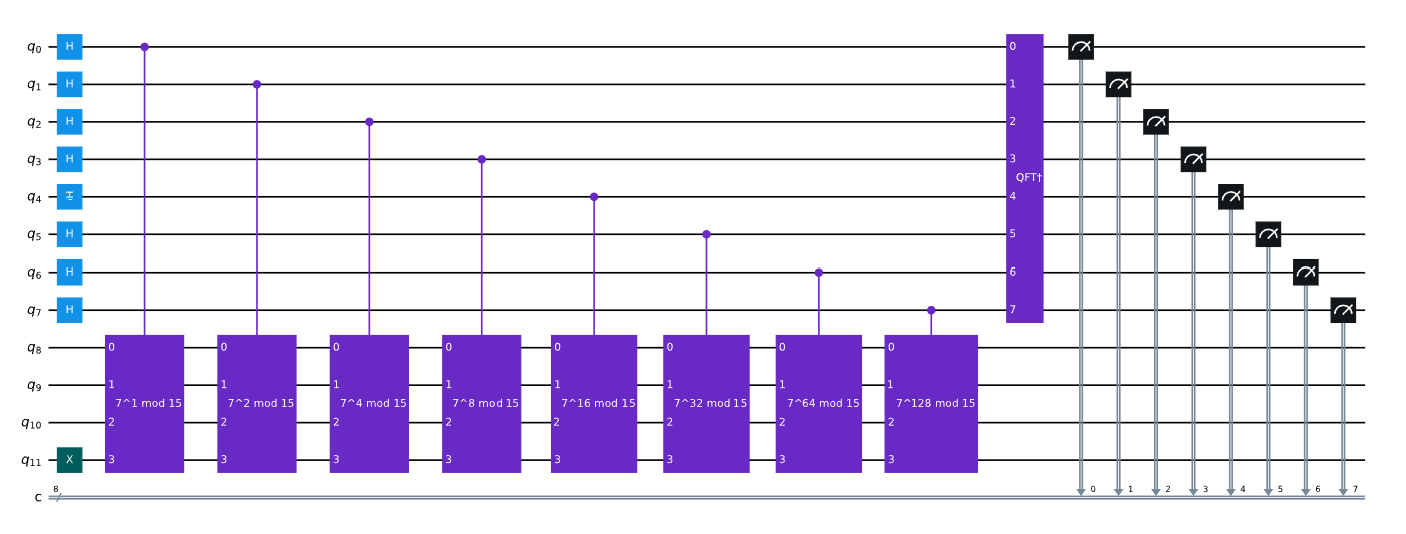
We can analyse codes provided by Qiskit in the future..
If we get a result phase \(0.50\), we can guess that r is 2 or 4. Then we may get a result pahse \(0.25\), we can guess that r is 4. The easiest solution to this is to simply repeat the experiment until we get a satisfying result for r.
4. How to do prime factoring?
Algorithm: Reduction of factoring to order-finding Inputs: A composite number \(N\) Outputs: A non-trivial factor of \(N\). Runtime: \(O\left((\log N)^{3}\right)\) operations. Succeeds with probability \(O(1)\). Procedure:
- If \(N\) is even, return the factor 2 .
- Determine whether \(N=a^{b}\) for integers \(a \geq 1\) and \(b \geq 2\), and if so return the factor \(a\).
- Randomly choose \(x\) in the range 1 to \(N-1\). If \(\operatorname{gcd}(x, N)>1\) then return the factor \(\operatorname{gcd}(x, N)\).
- Use the order-finding subroutine to find the order \(r\) of \(x\) modulo \(N\).
- If \(r\) is even and \(x^{r / 2} \neq-1(\bmod N)\) then compute \(\operatorname{gcd}\left(x^{r / 2}-1, N\right)\) and \(\operatorname{gcd}\left(x^{r / 2}+1, N\right)\), and test to see if one of these is a non-trivial factor, returning that factor if so. Otherwise, the algorithm fails.
5. Summary
Reference:
1. Nielsen, Michael A., and Isaac Chuang. "Quantum computation and quantum information." (2002): 558-559.
2. Asfaw, Abraham, et al. "Learn quantum computation using qiskit." Accessed: Oct 24 (2020): 2020.
3. Susskind, Leonard, and Art Friedman. Quantum mechanics: the theoretical minimum. Basic Books, 2014.