1. Problem Statement
Given an unsorted array, how to find a specific element in the array?
- Example:
- Find data record in place i
- Search Hash function: find x s.t. \(h(x)=y\)
- Find the best strategy
In quantum computing world, it would be a system that has following states:
\[\vert 1 \rangle \vert f(1) \rangle + \vert 2 \rangle \vert f(2) \rangle + ··· + \vert N \rangle \vert f(N) \rangle\]Then how can we get a measurement result of exact \(f(i)\)? It is not easy to find that the probability of getting \(f(i)\) is \(1/N\) now .
Now we use mathmatical language to describe this problem:
- Input: \(f:(0,1,...,N-1)->\{0,1\}\) with promise that there exists exactly one j s.t. \(f(j)=1\).
- Output: j
2. Quantum Computing Solution
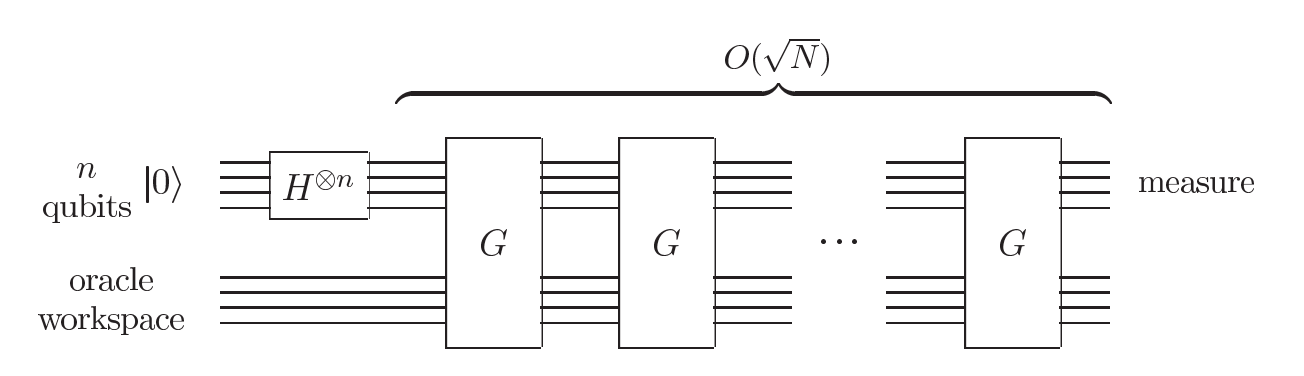
The following figure shows schematic circuit for the quantum search algorithm, in which we can see there are \(\sqrt{n}\) circuit G. Oracle workplace would be used to load f(x) on the register.
The following figure shows circuit details. In the oracle function, we use f(x) to distinguish amplititude of between targeted \(\vert j \rangle\) and other states.
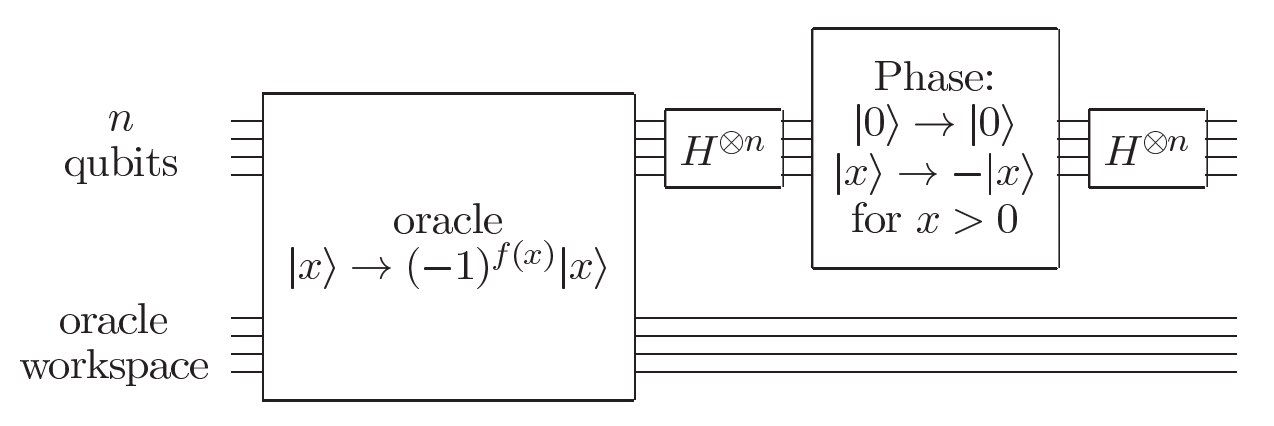
Then we would use a inverse mean function. Each of the operations in the Grover iteration may be efficiently implemented on a quantum computer. Steps 2 and 4, the Hadamard transforms, require \(n=\log (N)\) operations each. Step 3 , the conditional phase shift, may be implemented using the techniques of Section 4.3, using \(O(n)\) gates. The cost of the oracle call depends upon the specific application; It is useful to note that the combined effect of steps 2,3, and 4 is
\[H^{\otimes n}(2\vert 0\rangle\langle 0\vert -I) H^{\otimes n}=2\vert \psi\rangle\langle\psi\vert -I,\]where \(\vert \psi\rangle\) is the equally weighted superposition of states, (6.4). Thus the Grover iteration, \(G\), may be written \(G=(2\vert \psi\rangle\langle\psi\vert -I) O\).
We would implement \(G\) by nearly \(\sqrt{n}\) times.
What can G do:
Let us see that the operation \((2\vert \psi\rangle\langle\psi\vert -I)\) applied to a general state \(\sum_{k} \alpha_{k}\vert k\rangle\).
\[(2\vert \psi\rangle\langle\psi\vert -I) \sum_{k} \alpha_{k}\vert k\rangle \\ = \sum_{k}(-\alpha_{k} \vert k \rangle ) + \sum_{k} \frac{2\alpha_{k}}{N}\vert k \rangle \\ =\sum_{k}\left[-\alpha_{k}+2\langle\alpha\rangle\right]\vert k\rangle\]This operation is sometimes referred to as the inversion about mean operation.
3. Visualization
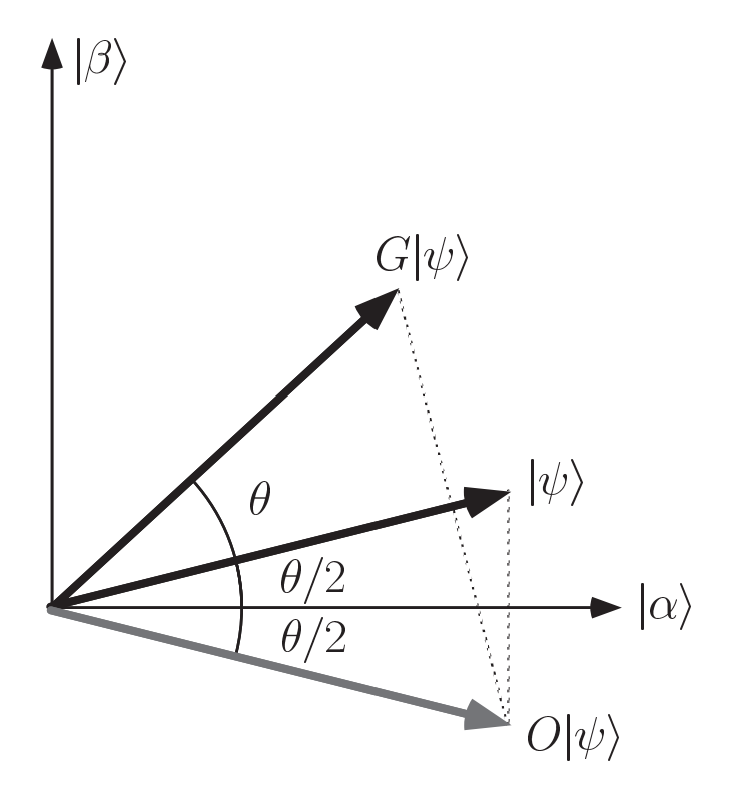
In this figure, dimension \(\vert \alpha \rangle\) is all dimensions but \(\vert \beta \rangle\) . For general Hilbert Space, \(\vert \alpha \rangle\) is orthogonal to \(\vert \beta \rangle\).
The oracle function is like a a reflection function about the vector \(\vert\alpha\rangle\). That is, \(O(a\vert \alpha\rangle+b\vert \beta\rangle)=a\vert \alpha\rangle-b\vert \beta\rangle\).
Similarly, \(2\vert \psi\rangle\langle\psi\vert -I\) also performs a reflection in the plane defined by \(\vert \alpha\rangle\) and \(\vert \beta\rangle\), about the vector \(\vert \psi\rangle\).
\[\vert \psi\rangle= \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1}\vert k \rangle\] \[\vert \alpha\rangle = \frac{1}{\sqrt{N-1}} \sum_{k=0, k\neq j}^{N-1}\vert k \rangle\]Then we can compute \(\theta\).
\[cos\frac{\theta}{2} = \langle \alpha \vert \psi\rangle = \frac{\sqrt{N-1}}{\sqrt{N}}\] \[\theta = 2arcsin \frac{1}{\sqrt{N}} \approx \frac{2}{\sqrt{N}}\]We expect that the last state of our system pointing to the \(\vert \beta \rangle\) direction. Therefore, the biggest times of do \(G\) operation is
\[\frac{\pi}{2} / \theta = \frac{\pi}{4}\sqrt{N}\]That is why we think the complexity of Grover algorithm is \(\sqrt{N}\).
4. Summary
Grover Algorithm can help to find specific value in an unsorted array, with quadratic speedup.
- Comlexity:
- Classical Algorithm: \(\Omega(n)\)
- Quantum Algorithm: \(O(\sqrt{n})\)
5. Qiskit Implementation
Reference:
1. Nielsen, Michael A., and Isaac Chuang. "Quantum computation and quantum information." (2002): 558-559.
2. Asfaw, Abraham, et al. "Learn quantum computation using qiskit." Accessed: Oct 24 (2020): 2020.
3. Susskind, Leonard, and Art Friedman. Quantum mechanics: the theoretical minimum. Basic Books, 2014.