Generally speaking, if you do not want to dig into details of quantum phase estimation, all you need to know is:
\[\frac{1}{2^{t / 2}} \sum_{j=0}^{2^{t}-1} e^{2 \pi i \varphi j}\vert j\rangle\vert u\rangle \rightarrow\vert \tilde{\varphi}\rangle\vert u\rangle\]that quantum phase estimation could transfer phase information into state.
1. Review of Quantum Fourier Transform
We first review what quantum fourier transform can do:
QFT can be expressed as the map:
\[\vert j\rangle \mapsto \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} e^{\frac{i 2\pi j k}{N}}\vert k\rangle\]Or the unitary matrix:
\[U_{Q F T}=\frac{1}{\sqrt{N}} \sum_{j=0}^{N-1} \sum_{k=0}^{N-1} e^{\frac{i 2\pi j k}{N}}\vert k\rangle\langle j\vert\]Quantum Fourier Transform achieves following transform:
\(\mid\) State in Computational Basis \(\rangle\) \(\stackrel{\text { QFT }}{\rightarrow} \quad\) \(\mid\) State in Fourier Basis \(\rangle\)
\[\mathrm{QFT}\vert x\rangle=\vert \tilde{x}\rangle\]states in the Fourier basis using the tilde (~)).
How about inverse quantum fourier transform:
IQFT can be expressed as the map:
\[\vert j\rangle \mapsto \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} e^{-\frac{i 2\pi j k}{N}}\vert k\rangle\]Or the unitary matrix: \(U_{Q F T}=\frac{1}{\sqrt{N}} \sum_{j=0}^{N-1} \sum_{k=0}^{N-1} e^{-\frac{i 2\pi j k}{N}}\vert k\rangle\langle j\vert\)
2. Quantum Phase Estimation Circuit
The following figure shows how quantum phase estimation works:
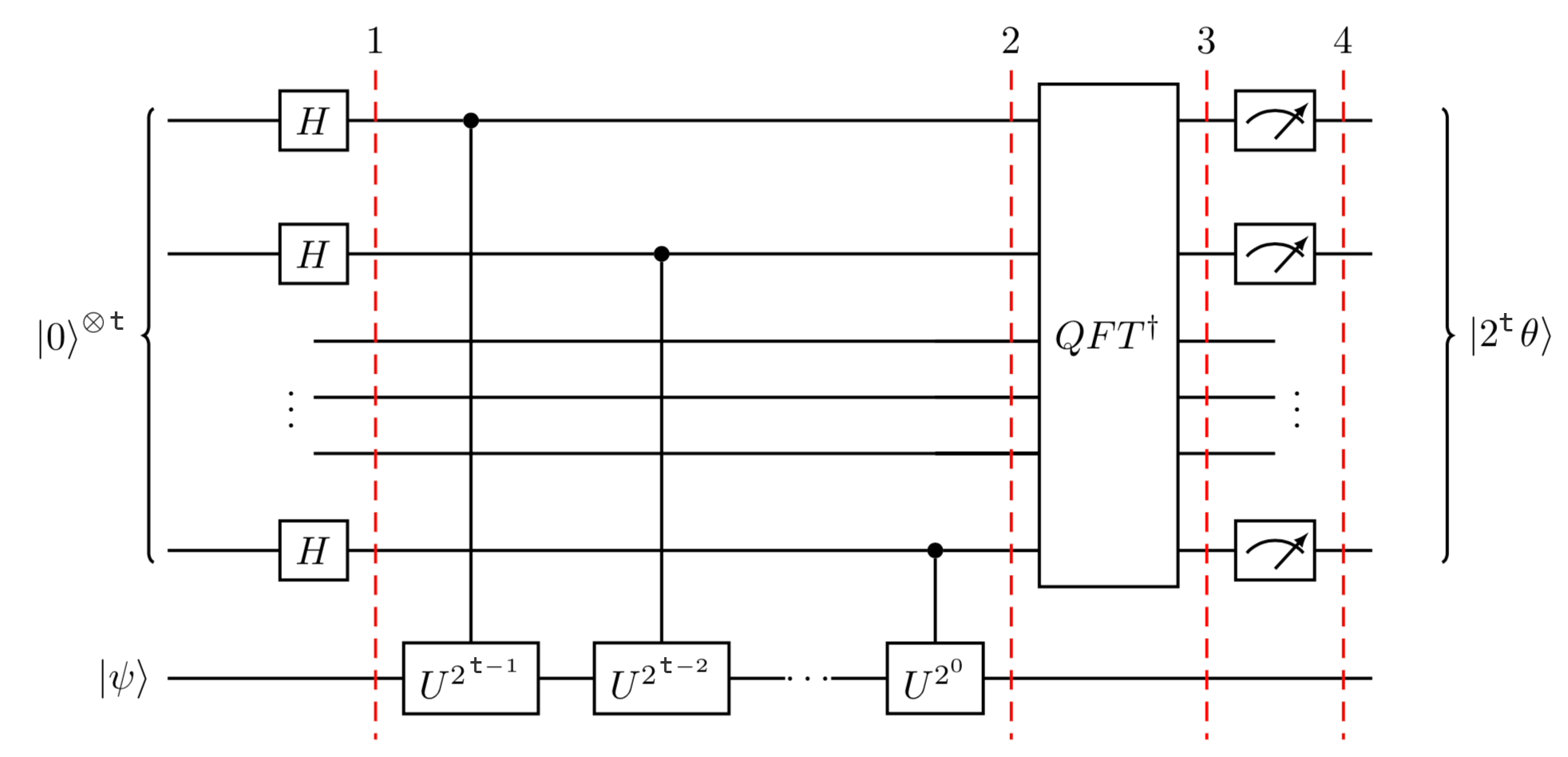
i. Setup: \(\vert \psi\rangle\) is in one set of qubit registers. An additional set of \(\mathrm{n}\) qubits form the counting register on which we will store the value \(2^{n} \theta\) : \(\psi_{0}=\vert 0\rangle^{\otimes} \pi\vert \psi\rangle\)
ii. Superposition: Apply a n-bit Hadamard gate operation \(H^{2 n}\) on the counting register:
\[\psi_{1}=\frac{1}{2^{\frac{n}{2}}}(\vert 0\rangle+\vert 1\rangle)^{\otimes n}\vert \psi\rangle\]iii. Controlled Unitary Operations: We need to introduce the controlled unitary C-U that applies the unitary operator U on the target register only if its corresponding control bit is \(\vert 1\rangle\). Since \(U\) is a unitary operator with eigenvector \(\ket{\psi}\) such that \(U\vert \psi\rangle=\) \(e^{2 \pi i \theta}\vert \psi\rangle\), this means:
\[U^{2 j}\vert \psi\rangle=U^{2^{j}-1} U\vert \psi\rangle=U^{2^{j}-1} e^{2 \pi i \theta}\vert \psi\rangle=\cdots=e^{2 \pi i 2^{j} \theta}\vert \psi\rangle\]Applying all the \(\mathrm{n}\) controlled operations \(\mathrm{C}-U^{2 j}\) with \(0 \leq j \leq n-1\), and using the relation \(\vert 0\rangle \otimes\vert \psi\rangle+\vert 1\rangle \otimes e^{2 \pi i \theta}\vert \psi\rangle=\) \(\left(\vert 0\rangle+e^{2 \pi i \theta}\vert 1\rangle\right) \otimes\vert \psi\rangle\)
\[\begin{aligned} \psi_{2} &=\frac{1}{2^{\frac{\pi}{2}}}\left(\vert 0\rangle+e^{2 \pi i \theta 2^{n-1}}\vert 1\rangle\right) \otimes \cdots \otimes\left(\vert 0\rangle+e^{2 \pi i \theta 2^{1}}\vert 1\rangle\right) \otimes\left(\vert 0\rangle+e^{2 \pi i \theta 2^{0}}\vert 1\rangle\right) \otimes\vert \psi\rangle \\ &=\frac{1}{2} \sum_{k=0}^{2^{n}-1} e^{2 \pi i \theta k}\vert k\rangle \otimes\vert \psi\rangle \end{aligned}\]where \(k\) denotes the integer representation of \(n\) -bit binary numbers. iv. Inverse Fourier Transform: Notice that the above expression is exactly the result of applying a quantum Fourier transform as we derived in the notebook on Quantum Fourier Transform and its Qiskit Implementation. Recall that QFT maps an n-qubit input state \(\ket{x}\) into an output as
\[Q F T\vert x\rangle=\frac{1}{2^{\frac{\pi}{2}}}\left(\vert 0\rangle+e^{\frac{2 \pi i}{2} x}\vert 1\rangle\right) \otimes\left(\vert 0\rangle+e^{\frac{2 \pi i}{2} x}\vert 1\rangle\right) \otimes \ldots \otimes\left(\vert 0\rangle+e^{\frac{2 \pi i}{2 \pi-1} x}\vert 1\rangle\right) \otimes\left(\vert 0\rangle+e^{\frac{2 \pi i}{2 t}}\vert 1\rangle\right)\]Replacing \(x\) by \(2^{n} \theta\) in the above expression gives exactly the expression derived in step 2 above. Therefore, to recover the state \(\left\vert 2^{n} \theta\right\rangle\), apply an inverse Fourier transform on the auxiliary register. Doing so, we find
\[\left\vert \psi_{3}\right\rangle=\frac{1}{2^{\frac{1}{2}}} \sum_{k=0}^{2^{n}-1} e^{2 \pi i \theta k}\vert k\rangle \otimes\vert \psi\rangle \stackrel{\operatorname{QFT}^{-1}}{\longrightarrow} \frac{1}{2^{n}} \sum_{x=0}^{2^{n}-1} \sum_{k=0}^{2^{n}-1} e^{-\frac{3 \pi i k}{2^{k}}\left(x-2^{n} \theta\right)}\vert x\rangle \otimes\vert \psi\rangle\]v. Measurement: The above expression peaks near \(x=2^{n} \theta\). For the case when \(2^{n} \theta\) is an integer, measuring in the computational basis gives the phase in the auxiliary register with high probability:
\[\left\vert \psi_{4}\right\rangle=\left\vert 2^{n} \theta\right\rangle \otimes\vert \psi\rangle\]Until now, we can find that the eigenvalue \(\theta\) already presents on the state.
3. Summary
Generally, we would use \(U\) as an observables to decribe the system. Therefore, eigenvalues may be expected to be input into state information and join computation. Then we can leverage quantum phase estimation to make eigenvalue into state information.
Quantum phase estimation would be one part of complex quantum algorithm, which we would further dig into in the next few articles.
Reference:
1. Nielsen, Michael A., and Isaac Chuang. "Quantum computation and quantum information." (2002): 558-559.
2. Asfaw, Abraham, et al. "Learn quantum computation using qiskit." Accessed: Oct 24 (2020): 2020.
3. Susskind, Leonard, and Art Friedman. Quantum mechanics: the theoretical minimum. Basic Books, 2014.