The Deutsch-Jozsa algorithm, which was originally presented in the seminal work of Deutsch and Jozsa (1992), stands as the pioneering quantum algorithm that outperforms the most efficient classical algorithms. This groundbreaking algorithm highlights the prospect of leveraging quantum computing as a powerful computational tool for specific problem classes, where classical computing may fail to provide the optimal solution. In this exposition, we will methodically explicate the Deutsch Algorithm and subsequently delve into the intricacies of the Deutsch-Jozsa algorithm.
1. Deutsch Algorithm
1.1 Problem Statement
The Deutsch-Jozsa algorithm addresses the problem of determining whether a given function f(x), where x ∈ {0,1}, is constant or balanced. A balanced function implies that f(0)≠f(1) and has two possible cases: f(0)=0, f(1)=1, or f(0)=1, f(1)=0. On the other hand, a constant function means that f(0)=f(1) and also has two possibilities: f(0)=f(1)=0 or f(0)=f(1)=1.
Given a function \(f(x), x\in\{0,1\}\), how can we know whether f(x) is a balanced function or constant function?
We first dig into what is the balanced function and constant function are.
- Balanced Function means \(f(0)\ne f(1)\), including two possibilites:
- \[f(0) = 0, f(1) = 1\]
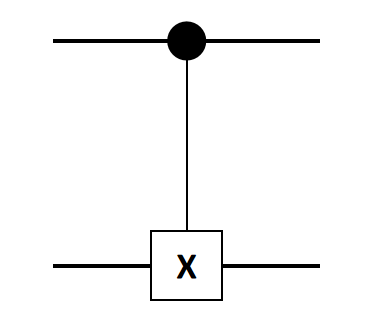
- \[f(0) = 1, f(1) = 0\]
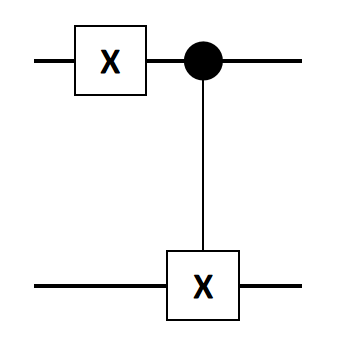
- Constant Function means \(f(0)= f(1)\), including two possibilites:
- \[f(0) = f(1) = 0\]

- \[f(0) = f(1) = 1\]
1.2 Solution Circuit
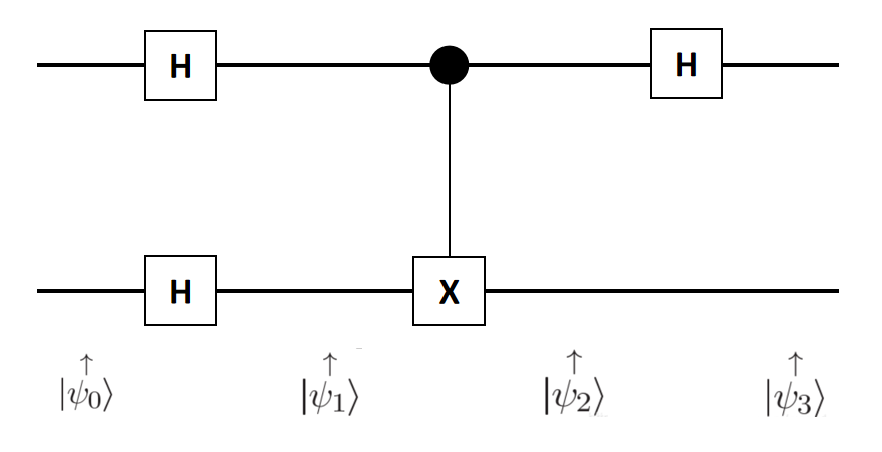
The Deutsch-Jozsa algorithm employs a solution circuit that utilizes a quantum computer’s unique capabilities to solve this problem. The solution circuit involves a series of steps that manipulate the quantum states to obtain the desired solution. In the circuit diagram presented, where n=1 in the upper register, a Hadamard gate is used to achieve superposition of quantum states. The targeted function is then used to obtain a modified quantum state that is subjected to another Hadamard gate. The resulting quantum state is measured to obtain the desired output.
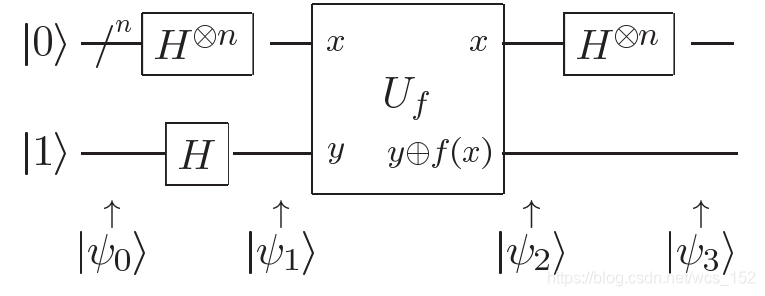
The following figure shows how we deduce from the beginning to the end. (I will spend some time using markdown to compile it in the future :).)
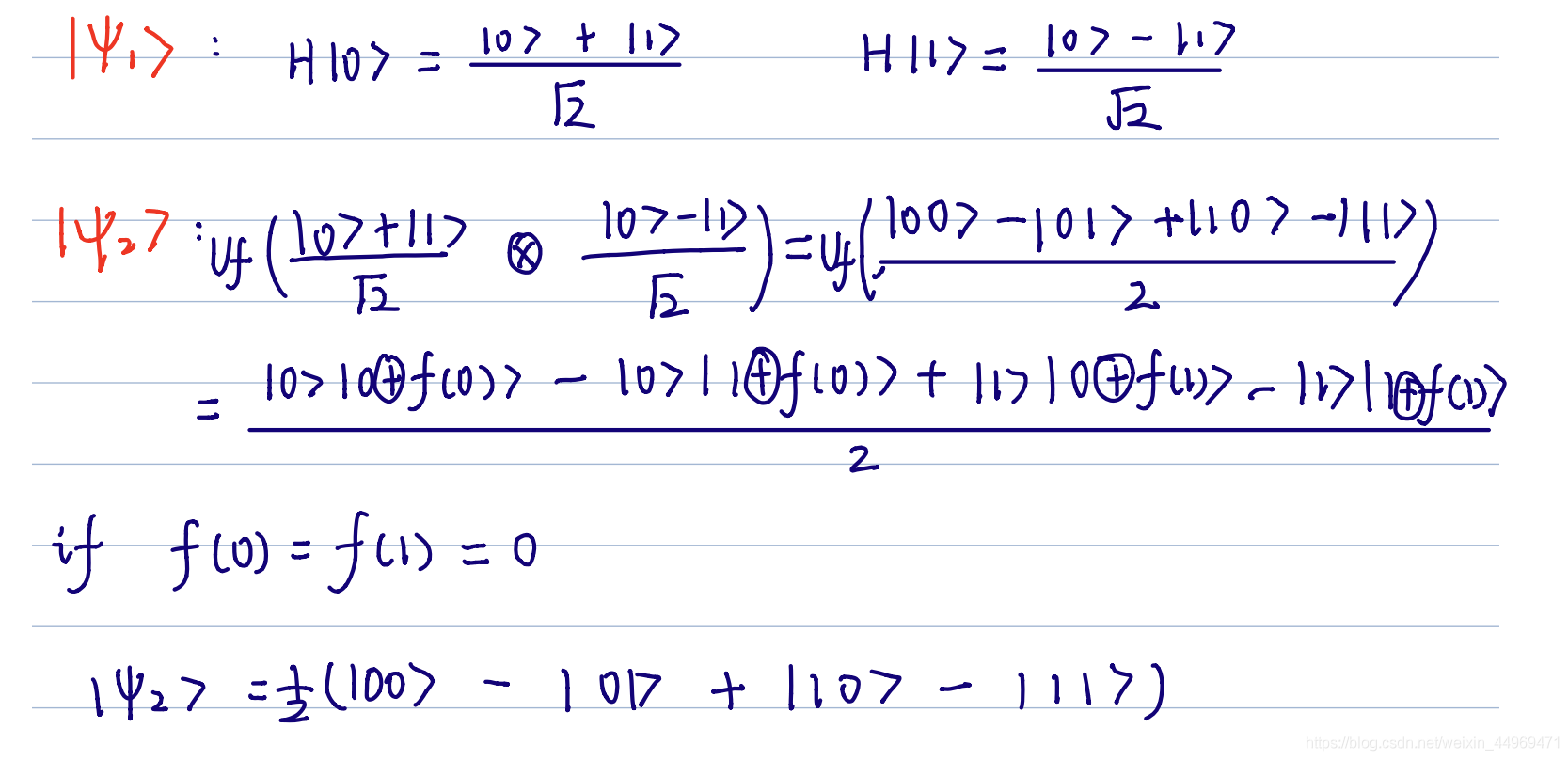
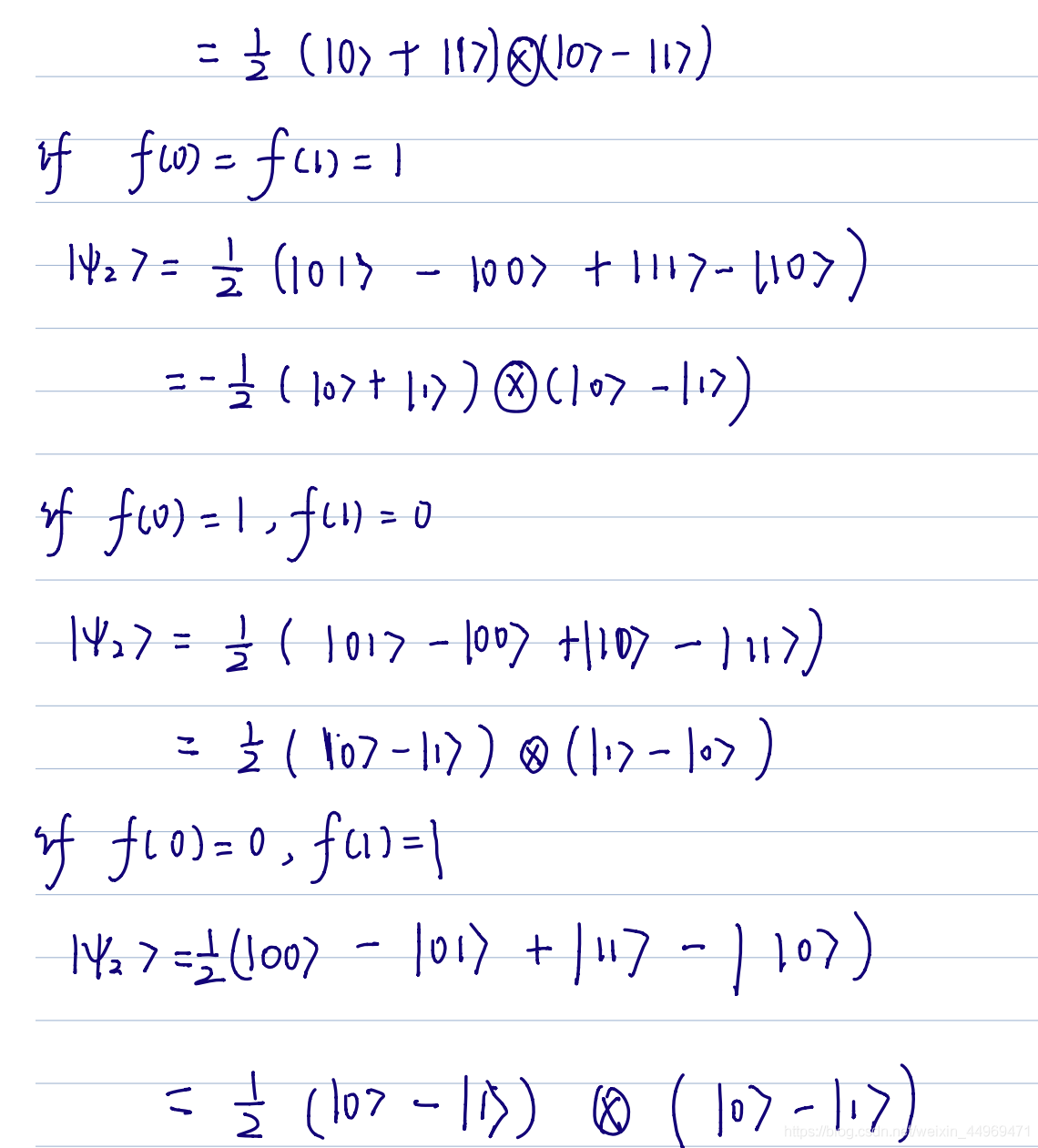

1.3 Example Circuit
The balanced function is used as an example to illustrate how the Deutsch-Jozsa algorithm works. The results obtained from the circuit for the balanced function show that the first register’s result is 1. In contrast, the constant function’s result will be 0. Therefore, the Deutsch-Jozsa algorithm can determine whether a given function is constant or balanced in a single measurement, whereas classical computing requires two measurements.
- Balanced Function One
The process goes like this:
\[\begin{aligned} &\left\vert \psi_{0}\right\rangle=\vert 01\rangle \\ &\left\vert \psi_{1}\right\rangle=\left[\frac{\vert 0\rangle+\vert 1\rangle}{\sqrt{2}}\right]\left[\frac{\vert 0\rangle-\vert 1\rangle}{\sqrt{2}}\right] \\ &\left\vert \psi_{2}\right\rangle=\frac{1}{2}(\vert 0\rangle-\vert 1\rangle)(\vert 0\rangle-\vert 1\rangle) \\ &\left\vert \psi_{3}\right\rangle=\frac{1}{2}\vert 1\rangle(\vert 0\rangle-\vert 1\rangle) \end{aligned}\]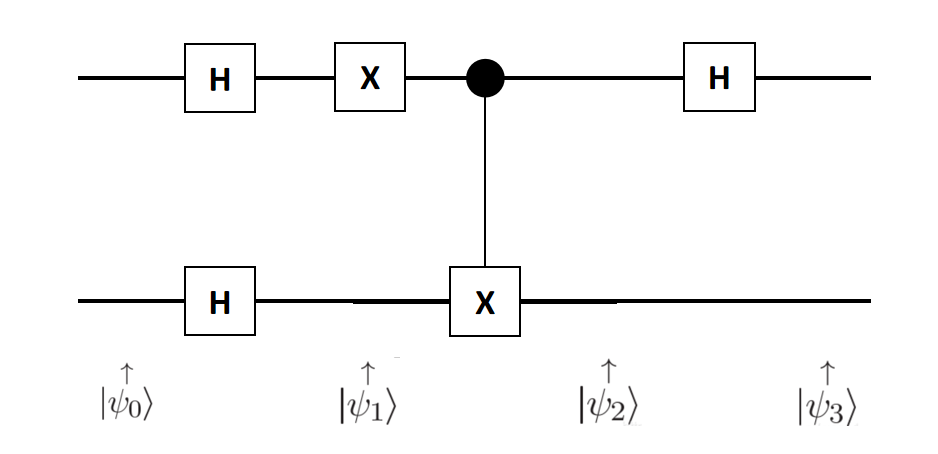
The process goes like this:
\[\begin{aligned} &\left\vert \psi_{0}\right\rangle=\vert 01\rangle \\ &\left\vert \psi_{1}\right\rangle=\left[\frac{\vert 0\rangle+\vert 1\rangle}{\sqrt{2}}\right]\left[\frac{\vert 0\rangle-\vert 1\rangle}{\sqrt{2}}\right] \\ &\left\vert \psi_{2}\right\rangle=\frac{1}{2}(\vert 0\rangle-\vert 1\rangle)(-\vert 0\rangle+\vert 1\rangle) \\ &\left\vert \psi_{3}\right\rangle=\frac{1}{2}\vert 1\rangle(-\vert 0\rangle+\vert 1\rangle) \end{aligned}\]We can find that the results of the first register in two circuits are \(\vert 1\rangle\). Similarly, if we use the constant function as an example, the result will be \(\vert 0\rangle\). So that’s what Deutsch can do to solve this problem.
By only one measurement, we can know whether a function is balanced or constant, while in the classical computing world, we need twice to see the result.
2. Deutsch-Jozsa Algorithm
The Deutsch-Jozsa algorithm is an extension of the Deutsch algorithm to n dimensions. The algorithm involves state preparation, superposition using the Hadamard gate, targeted function, and a second Hadamard gate. The resulting quantum state is then measured to obtain the solution. In the case of a constant function, the amplitude for the $\vert 0\rangle$ n state is either +1 or -1, depending on the constant value of f(x). All other amplitudes in the state are zero, resulting in observation yielding 0s for all qubits in the query register. If the function is balanced, the amplitude for the $\vert 0\rangle$ n state is zero, and measurement must yield a result other than 0 on at least one qubit in the query register.
The algorithm goes with the following procedures:
- State Preparation \(\left\vert \psi_{0}\right\rangle=\vert 0\rangle^{\otimes n}\vert 1\rangle\)
- Superposition by using Hardmard Gate \(\left\vert \psi_{1}\right\rangle=\sum_{x \in\{0,1\}^{n}} \frac{\vert x\rangle}{\sqrt{2^{n}}}\left[\frac{\vert 0\rangle-\vert 1\rangle}{\sqrt{2}}\right]\)
-
Use targeted function in the circuit \(\left\vert \psi_{2}\right\rangle=\sum_{x} \frac{(-1)^{f(x)}\vert x\rangle}{\sqrt{2^{n}}}\left[\frac{\vert 0\rangle-\vert 1\rangle}{\sqrt{2}}\right]\)
- Another Hardmard Gate \(H^{\otimes n}\)
to the first register. \(\left\vert \psi_{3}\right\rangle=\sum_{z} \sum_{x} \frac{(-1)^{x \cdot z+f(x)}\vert z\rangle}{2^{n}}\left[\frac{\vert 0\rangle-\vert 1\rangle}{\sqrt{2}}\right]\)
- Measurement. Note that the amplitude of the state \(\vert 0\rangle^{\otimes n}\) is \(\sum_{x}(-1)^{f(x)} / 2^{n}\)
Let’s look at the two possible cases \(f\) constant and \(f\) balanced \(-\) to discern what happens. In the case where \(f\) is constant the amplitude for \(\vert 0\rangle^{\otimes n}\) is \(+1\) or \(-1\), depending on the constant value \(f(x)\) takes. Because \(\left\vert \psi_{3}\right\rangle\) is of unit length, it follows that all the other amplitudes must be zero, and observation will yield 0s for all qubits in the query register.
If \(f\) is balanced, then the positive and negative contributions to the amplitude for \(\vert 0\rangle^{\otimes n}\) cancel, leaving an amplitude of zero, and measurement must yield a result other than 0 on at least one qubit in the query register.
Reference:
1. Nielsen, Michael A., and Isaac Chuang. "Quantum computation and quantum information." (2002): 558-559.
2. Asfaw, Abraham, et al. "Learn quantum computation using qiskit." Accessed: Oct 24 (2020): 2020.
3. Susskind, Leonard, and Art Friedman. Quantum mechanics: the theoretical minimum. Basic Books, 2014.