Quantum Proof of Work

1. Quantum Proof of Work Overview

Bitcoin’s Proof of Work prevents the double-spend and the Sybil attack very well. However, it consumes a large volume of energy.

2. Quantum Proof of Work Workflow

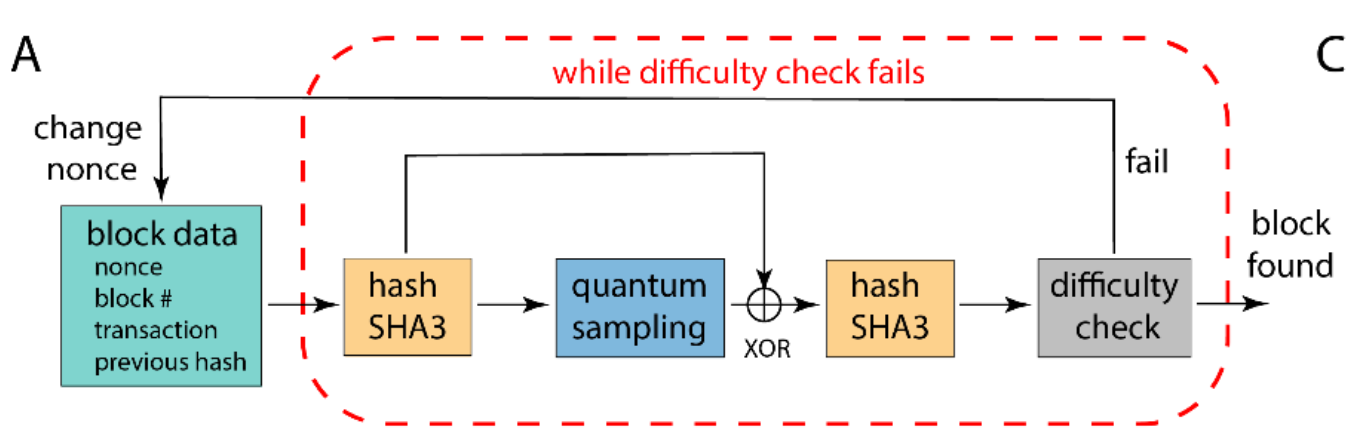
The input data (‘text’) is a concatenated string containing: nonce, transaction information and a hash string from a previous block. A nonce is a 32-bit randomly generated integer; transaction information is a ledger entry. By SHA3 algorithm the ‘text’ is transformed into a 256-bit hash-string that is then pushed through the qPoW stages. After the second hash module, we have a 256-bit hash-string as an output. If the output satisfies the conditions set by the task difficulty, i.e. the output string starts from a certain number of zeros, then the block is reported to be successfully mined. Otherwise, the output string is discarded and a new nonce is randomly generated for the next mining cycle. When the block is finally found (i.e., the difficulty check is passed), it goes through a verification test performed by a quantum simulator ran on a classical computer.

3. Highlight

We tested a 4-qubit ansatz on a publicly available 5-qubit processor (ibmq_quito) and found that the runtime of qPoW on ibmq_quito is nearly 100 times longer than on the simulator (qasm).

The quantum task was to find a maximum state of a pseudo-random quantum circuit with parametrized rotational gates.

From the quantum state distribution we select one state with the maximum probability.

4. Quantum Circuit Deep In

 # setting the quantum circuit:
    def quantum_circuit(q_par, n_qreg):
        qreg_q = QuantumRegister(n_qreg, 'q')
        creg_c = ClassicalRegister(n_qreg, 'c')
        circuit = QuantumCircuit(qreg_q, creg_c)

        #repetitive circuit
#         for i in range(circ_layer):
            
        #n-qubit circuit  
        k = 0 #counter for the parameter values
        for i in range(n_qreg):   
            circuit.rx(q_par[k+i]*pi/8, qreg_q[i])
        k+=n_qreg
        
        for i in range(n_qreg):    
            circuit.rz(q_par[k+i]*pi/8, qreg_q[i])
        k+=n_qreg
        
        for i in range(n_qreg):
            for j in range(n_qreg):
                if j != i:
                    circuit.crx(q_par[k+j]*pi/8, qreg_q[n_qreg-1-i], qreg_q[n_qreg-1-j])
                else:
                    k-=1
            k+=n_qreg-1
        
        for i in range(n_qreg):   
            circuit.rx(q_par[k+i]*pi/8, qreg_q[i])
        k+=n_qreg
        
        for i in range(n_qreg):    
            circuit.rz(q_par[k+i]*pi/8, qreg_q[i])

        #measurements of all qubits
        for i in range(len(qreg_q)):
            circuit.measure(qreg_q[i], creg_c[i])
        
        return circuit

5. Summary

Quantum proof of work uses quantum tasks to add difficuity to the overall task. Classical computers can not simulate the tasks easily and solve it. Therefore, people have to use real quantum computers to mine new blocks.

Reference:

1. Nielsen, Michael A., and Isaac Chuang. "Quantum computation and quantum information." (2002): 558-559.

2. M. Y. Shalaginov and M. Dubrovsky, “Quantum Proof of Work with Parametrized Quantum Circuits,” p. 6.