Practical Byzantine Fault Tolerance

Practical Byzantine Fault Tolerance (PBFT) is a robust algorithm that can continue to function even if up to 1/3 of the machines in a network fail in any way.

The image below illustrates how the PBFT state machine processes requests [1].

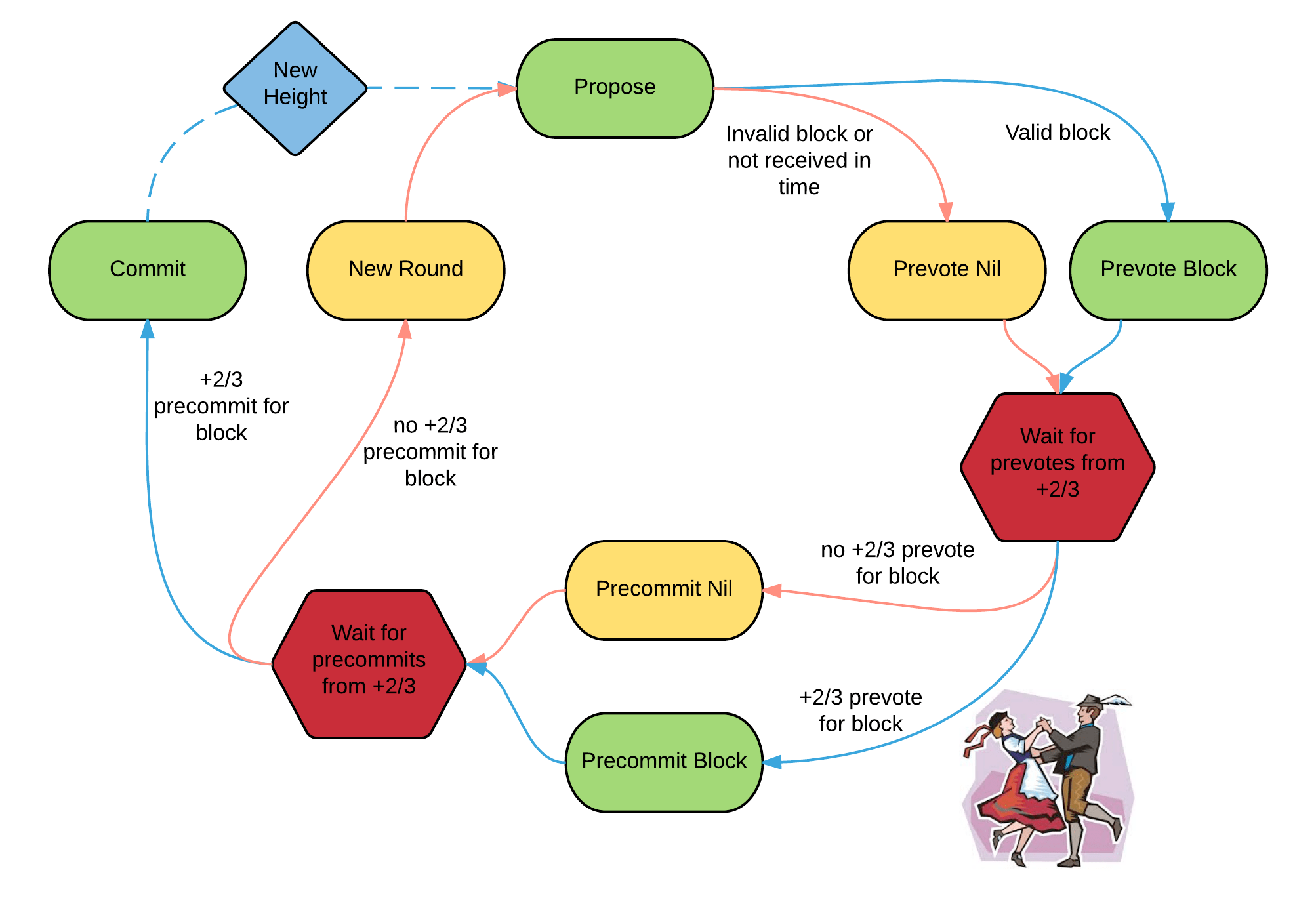
In the worst-case scenario, where 1/3 of the machines (denoted as “f”) are normal machines that have failed, PBFT still works effectively because there are still more normal machines (1 + f) than malicious machines (f). During the request processing, normal machines take the lead and PBFT can still function even if the network has f malicious machines.

Normal machines only need to wait for 1 + 2f responses instead of getting all prevotes and precommits in the process.

To formally prove why the number 1/3 is chosen, let’s assume we have a network of n machines, and the network can function well if f machines are malicious. In this case, there are n - f normal machines.

To ensure the network can function well, we need to determine the minimum number of votes (denoted as X) needed in each round. This is because malicious nodes may not vote and delay the decision-making process.

Therefore, X should not be greater than or equal to the number of normal machines (n - f). Additionally, to ensure that more than half of the votes come from normal machines, we need to satisfy the condition X/2 > f.

Combining these two conditions, we get n > 3f.

Reference:

1. Hitesh Malviya, "Develop PBFT Consensus based application on tendermint.", Available at: https://itsblockchain.com/develop-pbft-consensus-based-application-on-tendermint/